

En plus de votre inscription gratuite, recevez également :

Le plan d’investissement adaptable qui a permis à nos clients de réaliser en moyenne +120% de plus-values en 2023.
(d’une valeur de 250€)Calcul des intérêts composés et définition

Qualifiés de « 8ème merveille du monde » par Albert Einstein, les intérêts composés sont l’atout N°1 de tout investisseur. Ils constituent un avantage crucial pour l’investisseur patient, pourvu d’une faible préférence pour le présent, c’est-à-dire disposé à sacrifier une jouissance présente pour obtenir une jouissance à venir plus importante.
Souvent sous estimés, ils sont pourtant le fondement même des plus grandes fortunes comme celles de Warren Buffet, l’un des meilleurs investisseurs du XXème siècle. A l’inverse, s’ils sont mal compris ils peuvent présenter un risque non négligeable pour un portefeuille.
A travers cet article, les lecteurs comprendront à quel point il est avantageux de commencer à épargner et à investir le plus tôt possible dans sa vie. Pour ceux qui souhaitent faire du trading et même en vivre, ils constateront que les intérêts composés représentent l’arme ultime pour parvenir à ses fins.
Sommaire :
- Les intérêts composés en bourse : définition
- Quelle formule de calcul pour calculer les intérêts composés ?
- Les risques liés aux intérêts composés
- Comment profiter des intérêts composés en trading ?
Les intérêts composés en bourse : définition
Les intérêts composés sont le résultat d’un calcul d’intérêts qui intègre les intérêts passés. En d’autres termes les intérêts composés sont des intérêts sur les intérêts.
Ils se distinguent ainsi des intérêts simples, qui ne se calculent que sur la base du principal, tandis que les intérêts composés se calculent sur la base de ce dernier, auquel sont ajoutés tous les versements d’intérêts (en cas de prêt) ou les gains (en cas de profit) passés.
Leur progression est ainsi plus importante que celle des intérêts simples, car elle est géométrique et non arithmétique ; cette différence s’accroît à mesure que les périodes de composition passent.
Les intérêts composés sont la raison pour laquelle le temps est l’allié de l’investisseur. À taux nominal égal, plus le temps passe plus les rendements sont grands, non seulement en termes absolus, mais aussi relatifs vis-à-vis du principal initial.
En effet, un montant de 1 000 € placé à 4 % d’intérêt annuel ne rapportera que 40 € à la fin de la première année. Mais dès la seconde année, les 4 % ne se basent plus sur 1 000 €, mais sur 1 040 €, et ainsi de suite.
De sorte qu’au bout de 18 ans, le calcul se fait sur plus du double de la somme initiale, 2 025 € exactement. En pratique, cela signifie que les 4 % sur la somme finale sont équivalents à 8 % sur la somme initiale. Donc les rendements, tant absolus que relatifs, augmentent au cours du temps.
Quelle formule pour calculer les intérêts composés ?
La formule pour calculer valeur finale d’un portefeuille en fonction des intérêts perçus est la suivante :
Vf = Vi * (1 + r)^Z
Avec :
Vf : la valeur finale
Vi : la valeur initiale
r : le taux ou le rendement. Pour un taux de 3 % on notera 0,03
Z : le nombre de périodes de composition. Par exemple, pour des intérêts mensuels pendant un an : 12.
(Le signe ^ exprime la puissance : X^Y se lit donc comme X à la puissance Y)
Ainsi, si un tradeur emploie un capital initial de 10 000 €, et parvient à un taux de profit mensuel moyen de 2 % par mois sur 1 an, objectif tout à fait envisageable, nous obtenons le calcul suivant :
Vf = 100 00 * (1,02)^12
Soit Vf = 12 682 €
Composé sur 10 ans, et non plus un an, nous avons :
Vf = 10 000 * (1,02)^120
La somme initiale passe de 10 000 à un peu plus de 100 000 euros.
Pour calculer le taux d'intérêt nécessaire pour passer d’une valeur initiale à une valeur finale connue, on procédera comme suit :
r = [(Vf/Vi)^(1-Z)]-1
Pour calculer le nombre de périodes nécessaire pour passer d’une valeur initiale à une valeur finale avec un taux d'intérêt de Z, on procédera comme ceci :
Z = ln(Vf/Vi)/ln(1+r)]
ln désignant le logarithme népérien.
Pour simplifier les calculs, on pourra utiliser la règle des 72 qui permet de calculer le temps nécessaire pour doubler son capital en fonction d’un taux d'intérêt donné.
Il nous suffit pour cela de diviser 72 par le taux d'intérêt en question.
Par exemple, pour doubler un capital de 10 000 € avec un rendement de 1% par mois, 72 mois (72/1) seront nécessaires pour passer de 10 000 à 20 000.
En revanche, si l’on part d’un rendement de 1 à 2 % par mois en moyenne, 36 mois (72/2) seront nécessaires.
Les risques liés aux intérêts composés
Cependant, les intérêts composés ont deux versants, selon que l’on soit créanciers ou débiteurs. S’ils représentent un avantage certain pour les premiers, qui touchent les intérêts, ils sont au contraire un inconvénient pour les seconds.
Les inconvénients délétères des intérêts composés se font aussi sentir pour le simple particulier dépourvu d’investissement dans la mesure où l’inflation entame progressivement le pouvoir d’achat d’une monnaie. La perte du pouvoir d’achat d’une unité monétaire consiste effectivement en un intérêt composé inversé.
Ainsi, même un taux d’inflation de 2 %, jugé « raisonnable » par les banquiers centraux américains comme européens, suffit pour réduire considérablement un capital non investi au cours du temps.
En effet, en raison d’une perte de pouvoir d’achat de 2 % par an, il suffit de 25 ans pour qu’un capital de 100 000 € perde 40 % de son pouvoir d’achat. En d’autres mots, il suffit d’une génération pour que 100 000 € se transforme, à pouvoir d’achat constant, en 60 000 €.
La perte du pouvoir d’achat de dollar depuis l’instauration de la Réserve Fédérale américaine en 1913 – pourtant sans cessée lutter contre l’inflation – est flagrante : un produit coutant 100 $ en 1913 couterait aujourd’hui, en 2020, 2 625 dollars. Cela équivaut à une inflation cumulée – c’est-à-dire des intérêts composés inversés – s’élevant à 2 525 %.
Comment profiter des intérêts composés en trading ?
Les intérêts composés, bien que souvent sous estimés, sont parmi les armes les plus redoutables d’un trader. En effet, sur le long terme la différence entre un trader qui les utilisent et un qui n’en tire pas avantage est énorme.
Prenons l’exemple de deux traders plutôt doués, dotés de 10 000 € chacun, qui réussissent à faire une moyenne de 5% de gains par mois. Le premier a l’habitude de retirer ses gains pour se faire plaisir et s’offrir des biens matériels. Le second au contraire, préfère réinvestir ses gains dans son capital de trading tous les mois.
Voilà ce qu’on observe après seulement 5 ans de trading :
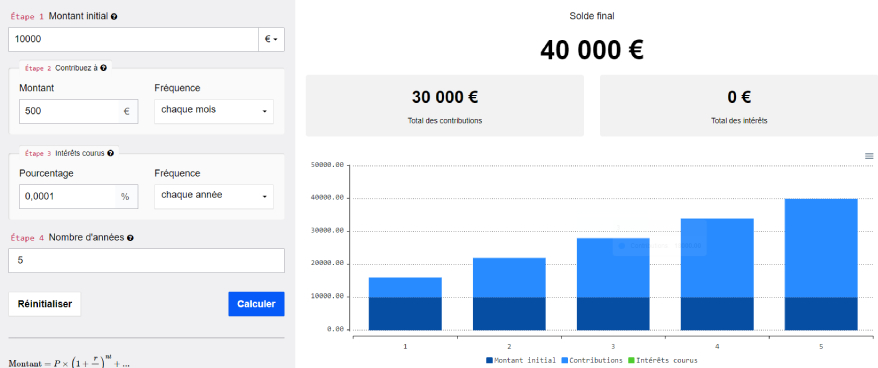
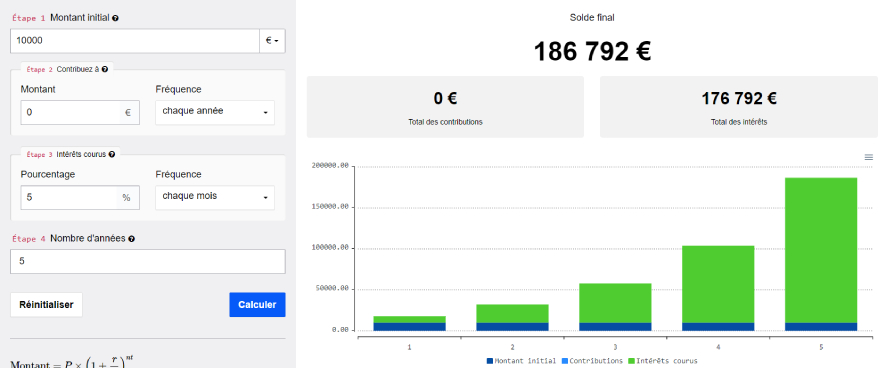
Le constat est édifiant : le trader qui a utilisé les intérêts composés a désormais un capital de trading de 186 792 € tandis que l’autre n’a accumulé que 40 000€ dans le même temps. En seulement 5 ans les intérêts composés font déjà une grosse différence, quand on sait que leur puissance ne s’exprime vraiment qu’avec le temps…
Il suffit donc, pour profiter des intérêts composés en trading, de réinvestir tous ses gains dans son capital. Ainsi, celui-ci grossira beaucoup plus rapidement avec le poids des années.
Pour rappel : Warren Buffet est devenu millionnaire à 30 ans et milliardaire à « seulement » 55 ans. En fait, 99% de sa fortune s’est faite après ses 50 ans. La raison ? Les intérêts composés qui créent un effet « boule de neige » avec le temps.

















